Parametric Equations Calculator: A Smart Tool for Complex Curves
Introduction to Parametric Equations
Parametric equations are a different way to describe curves. Instead of writing a relationship between x and y directly, both x and y are expressed in terms of a third variable, usually denoted as t. For example:
- x = cos(t)
- y = sin(t)
This set of equations draws a circle when t varies from 0 to 2π. However, solving and visualizing these equations by hand can be difficult. This is where the parametric equations calculator becomes extremely helpful.
What Is a Parametric Equations Calculator?
It allows users to enter functions for x(t) and y(t), define a range for the parameter t, and view a graphical representation of the resulting curve. Many advanced calculators also support additional functionalities like 3D plotting, derivative calculations, and step-by-step transformations.
Why Parametric Equations Matter
Traditional Cartesian equations, such as y = mx + b, are limited in describing complex curves, especially when modeling motion or curves with loops and direction changes. Parametric equations solve this limitation by giving more control and flexibility. They are particularly useful in:
- Simulating motion in physics
- Designing curved paths in engineering
- Creating animation paths in computer graphics
- Solving advanced calculus problems involving arc length and area
In each case, a parametric equations calculator simplifies the process by eliminating manual plotting or algebraic manipulation.
See also: Socratic Dialog: A Timeless Method for Deep Thinking
Key Features of a Parametric Equations Calculator
A good parametric equations calculator offers several key features, making it useful for students, teachers, professionals, and researchers alike.
Graphing Capabilities
One of the most useful functions is graph plotting. By inputting x(t) and y(t) along with a range for t, users can instantly see a visual representation of the curve.
Step-by-Step Solutions
Some calculators provide detailed steps that show how values are computed, helping users understand the math behind the scenes.
Parameter Range Customization
Users can define how the parameter t should vary, such as t = -5 to 5, or t = 0 to 2π, to observe different portions of the curve.
How to Use the Calculator
Here’s a step-by-step guide:
Step 1: Enter the Functions
Input your parametric equations. For example:
- x(t) = t
- y(t) = t²
Step 2: Choose the Range
Set the range for t, such as -10 to 10, depending on how much of the curve you want to view.
Step 3: Plot or Solve
Click on the “Calculate” or “Plot” button.
Step 4: Analyze Results
Study the curve to understand how x and y change as t varies. You may also get derivative information or Cartesian conversions depending on the tool.
Educational Benefits
For students learning about motion, calculus, or conic sections, parametric equations can initially seem confusing. A calculator helps in multiple ways:
- Visual Learning: See how changing the parameter affects the graph.
- Concept Clarity: Understand curve orientation and direction.
- Practice: Check homework problems or test preparation.
- Error Checking: Quickly verify whether manually solved problems are correct.
Engineering and Scientific Applications
In technical fields, parametric equations play a central role. Engineers use them to design and simulate systems where the position of an object changes over time. Examples include:
- Robotic arms following a specific path
- Projectile motion analysis
- Electrical signal plotting
- Fluid flow curves in mechanical systems
Using a parametric equations calculator makes these tasks more efficient by handling the math instantly.
Comparing Popular Calculators
Many parametric calculators are available online. Here are a few worth mentioning:
Desmos
Desmos is an intuitive and interactive graphing calculator that allows for parametric input. It’s great for real-time visualization and experimentation.
GeoGebra
GeoGebra provides a rich set of math tools for graphing, calculus, and geometry. It’s particularly suitable for educators and learners.
Symbolab
Symbolab provides detailed step-by-step solutions and is very useful for learning the logic behind the computations.
Wolfram Alpha
Wolfram Alpha offers symbolic computation and is ideal for users needing analytical results in addition to graphs.
Practical Example
Let’s consider a real-world example.
Equations:
- x(t) = 4cos(t)
- y(t) = 3sin(t)
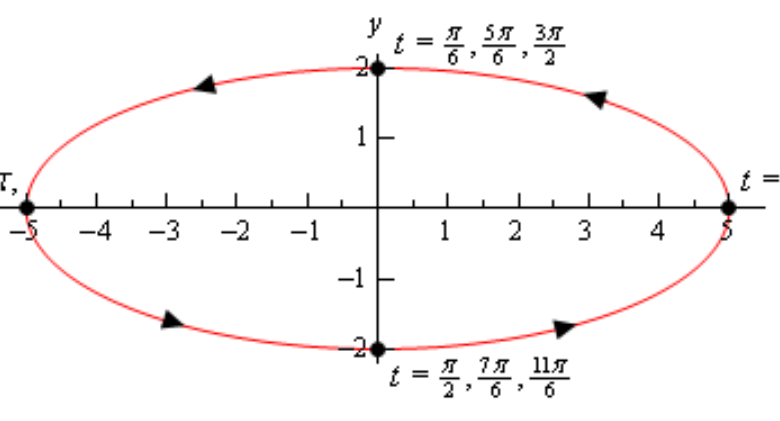
These equations describe an ellipse. Using a parametric equations calculator:
- Enter the functions above.
- Set t from 0 to 2π.
- Click to plot.
You can explore how changing the coefficients changes the ellipse’s shape.
Limitations and Cautions
While parametric calculators are powerful, users should still understand the theoryThe graph may not represent the entire function if the t range is too limited.
- Some curves may overlap or retrace paths, making visual interpretation tricky.
- Calculators may fail to convert parametric to Cartesian if algebraic simplification is complex or impossible.
Thus, combining tool usage with solid mathematical understanding leads to the best outcomes.
Conclusion
The parametric equations calculator is an indispensable resource for anyone dealing with advanced mathematical models. It simplifies plotting, speeds up problem-solving, and provides a deeper understanding of how parameterized curves behave. Whether you’re a student exploring algebra or a professional working with motion paths, this calculator empowers you to handle complex equations with ease.
If you’re looking to visualize curves, learn efficiently, or enhance your work in science and engineering, this tool is worth mastering. With just a few clicks, it unlocks a world of mathematical possibilities.