Circle Area from Diameter
Understanding how to work with circles is a fundamental skill in both academic mathematics and real-life situations. While many people are familiar with using the radius to calculate this, it’s just as important to know how to find the area of a circle with diameter directly. This method is especially useful when the diameter is the only available measurement.
What Is a Diameter?
A diameter is the straight line that passes through the center of the circle, touching both sides of the boundary.
Formula:
d = 2 × r
Knowing this relationship allows you to switch between diameter and radius easily, which is essential when using circle formulas.
Area of a Circle – Standard Approach
The conventional formula for the area of a circle involves the radius:
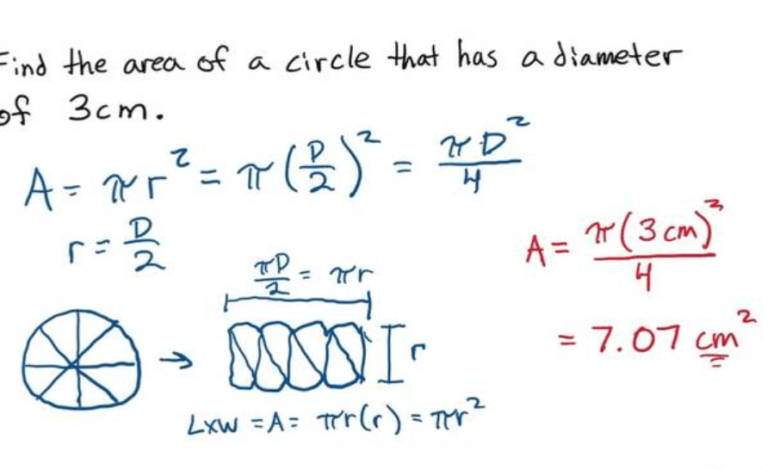
Area (A) = π × r²
However, if you are provided with the diameter, you can simply modify this formula by expressing the radius in terms of diameter.
Area Using Diameter – Derived Formula
Since radius is half of the diameter:
r = d ÷ 2
Substituting into the area formula:
A = π × (d ÷ 2)²
A = π × d² ÷ 4
So, the formula to find the area of a circle using its diameter becomes:
Area (A) = π × d² ÷ 4
This version is just as valid and often more convenient when the diameter is the given measurement.
Why Use Diameter?
In many practical settings, the diameter is easier to measure than the radius. For example:
- Measuring a dinner plate across its center
- Determining the width of a circular manhole cover
- Measuring the cross-section of a pipe
These real-world items often provide the full width (diameter), not the center-based distance (radius).
See also: Service Request Case: 6097102667
Practical Example
Let’s break down a full example.
Problem:
What is the area?
Step 1: Square the diameter
10² = 100
Step 2: Multiply by π (approximately 3.1416)
100 × 3.1416 = 314.16
Step 3: Divide by 4
314.16 ÷ 4 = 78.54
Answer:
The area of the circle is 78.54 cm²
Common Mistakes to Avoid
When learning how to find the area of a circle with diameter some common errors can affect the final result:
1. Forgetting to Divide the Diameter
Many students forget that the area formula is based on the radius squared, not diameter. If you plug the diameter directly into the standard formula without adjusting, you’ll get a result four times too large.
2. Squaring Incorrectly
Squaring the whole diameter before dividing by four is essential. Always apply the order of operations correctly.
3. Using Rounded π Too Early
Avoid rounding π at the beginning. Use the π key on your calculator or enter 3.1416 at the final step for better precision.
Applications in Real Life
This calculation is not just for textbooks—it’s used in countless industries and fields:
Construction and Engineering
- Determining how much concrete is needed for circular foundations
- Calculating the surface area of cylindrical tanks or pillars
Manufacturing
- Designing circular machine parts
- Estimating the material required to produce round objects
Daily Life
- Finding the surface area of circular tables or rugs
- Estimating how much paint is needed for a circular sign or object
Knowing how to calculate area from diameter is a handy tool for solving practical problems quickly.
Comparing Radius and Diameter Approaches
To illustrate the relationship, let’s compare the same circle using both formulas:
Given:
Diameter = 8 cm
Radius = 4 cm
Using Radius:
A = π × r² = π × 16 ≈ 50.27 cm²
Using Diameter:
A = π × 8² ÷ 4 = π × 64 ÷ 4 = π × 16 ≈ 50.27 cm²
As shown, both methods provide the same result, proving the validity of the π × d² ÷ 4 formula.
Table of Sample Values
| Diameter (cm) | Area (cm²) |
| 2 | 3.14 |
| 4 | 12.57 |
| 6 | 28.27 |
| 8 | 50.27 |
| 10 | 78.54 |
These values show how the area grows rapidly as the diameter increases. This quadratic growth occurs because the diameter is squared in the formula.
Tips for Accurate Calculation
- Use a scientific calculator that includes π
- When working with large values, avoid early rounding
- Always double-check whether the given measurement is diameter or radius
Using Technology
If you’re using spreadsheet software like Excel or Google Sheets, you can automate area calculations from diameter with a simple formula.
Excel Example:
If cell A1 contains the diameter, use:
=PI() * A1^2 / 4
This saves time, especially when working with multiple values in batch calculations.
Practice Problems
Try these for better understanding:
Problem 1:
Solution:
16² = 256
256 × π = 804.25
804.25 ÷ 4 = 201.06 cm²
Problem 2:
You measure a pizza to be 30 cm across. What is its surface area?
Solution:
30² = 900
900 × π ≈ 2827.43
2827.43 ÷ 4 = 706.86 cm²
Final Thoughts
Knowing how to find the area of a circle with diameter empowers you to solve problems quickly and efficiently. While using the radius is the more common method, being able to work directly with the diameter simplifies many real-world calculations. Whether you’re a student, engineer, or hobbyist, mastering this technique adds versatility to your mathematical toolkit.
With just a squared diameter, some multiplication, and a basic understanding of π, you can calculate the area of any circle. Practice the formula, apply it to various scenarios, and you’ll become confident in using this approach with ease.